En este juego tenía la impresión de que ir a una batalla con mayorías era un beneficio bastante importante. Si iba con una ventaja de 4 estaba claro que la victoria era inevitable, pero, ¿cuánto aporta tener una sola tropa de ventaja?, ¿merece la pena ir con más (2, tal vez 3)?, ¿debo retirarme si estoy en desventaja?. Pues me puse a hacer los números y el resultado la verdad es que me sorprendió, pero me hizo ver de forma bastante nítida la intención de los creadores cuando pergeñaron el combate. Pero ya llegaremos a eso, primero vamos a ver cómo obtener respuestas...

Empezamos con las probabilidades de victoria, empate y derrota en una ronda cualquiera, en función del número de la fuerza del atacante y el defensor. Recordemos que en este juego cada contendiente lanza un dado (0, 1, 1, 2, 2, 3) y le suma al resultado el número de tropas que tiene en la batalla. El que obtenga el resultado más bajo, pierde una unidad. Si hay empate, ambos la pierden. Pues bien, aquí sólo hay que contar de los 36 posibles resultados de lanzar dos dados, cuantos se traducen en victorias, derrotas y empates después de sumar las tropas de cada equipo. Como todo el mundo sospechaba,  las probabilidades de victoria en una ronda sólo van a depender de la diferencia entre el número de unidades de atacante y defensor. Se aprecia claramente en las diagonales de las siguientes matrices, que están representando las probabilidades de victoria del ejército 1 (azul), del ejército 2 (rojo) o de empate (verde), donde las filas indican las tropas que tiene en batalla el ejército 1 y las columnas las que tiene el ejército 2:

PROBABILIDAD DE VICTORIA DE E1 (A)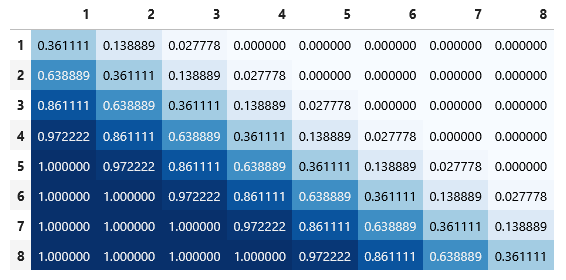

PROBABILIDAD DE VICTORIA DE E2 (B)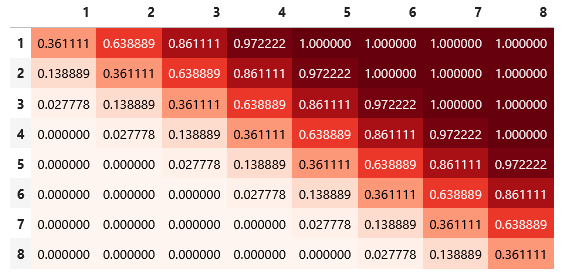

PROBABILIDAD DE EMPATE (C)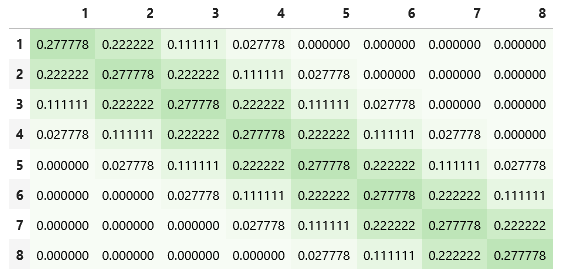


Ahora se pone interesante. Para responder a las preguntas iniciales no nos interesa tanto saber cuál es el resultado de una ronda en función del número de tropas, sino la probabilidad de que cada ejército gane finalmente la batalla (es decir, aniquile al rival) después de sucesivas rondas de combate y suponiendo que nadie se retira. Para evaluarlo hay que tener en consideración todos los posibles caminos que puede seguir una batalla. Para empezar, partimos de un campo de batalla V(n,m), donde n es el número de tropas del ejército 1 (E1) y m el del ejército 2 (E2). Así, por ejemplo, V(3,2) significaría que E1 tiene 3 tropas y E2 tiene 2.

Ahora vamos a ponerles nombre a los posibles resultados de la ronda (eventos):

• A. Significa que E1 gana la ronda. Por tanto V(n,m) pasa a ser V(n, m-1) después de A. O, de otra forma,     A: V(n,m) -> V(n, m-1)
• B. Significa que E2 gana la ronda. Por tanto V(n,m) pasa a ser V(n-1, m) después de B. O, de otra forma,     B: V(n,m) -> V(n-1, m)
• C. Significa que E1 y E2 empatan. Por tanto V(n,m) pasa a ser V(n-1, m-1) después de C. O, de otra forma,  C: V(n,m) -> V(n-1, m-1)

Pues bien, para calcular la probabilidad de que un ejército gane en una batalla partiendo de una determinada distribución de tropas (n,m), hay que:

• identificar todos los posibles caminos que puede seguir la batalla,
• obtener la probabilidad de cada camino (multiplicando las probabilidades de cada evento del camino: victoria (A)/derrota (B)/ empate (C), ya que son sucesos independientes) y
• sumar las probabilidades totales de aquellos caminos que conducen a la victoria del ejército considerado (probabilidad de la unión).

Con un ejemplo todo se ve más claro:
Supongamos que una batalla empieza con 2 tropas del ejército E1 y una tropa del ejército E2 y queremos saber la probabilidad de victoria de E1. La batalla puede seguir cinco posibles caminos, tres de ellos conducen a la victoria de E1 (azul), uno a la victoria de E2 (rojo) y otro al empate (verde):

• V(2,1) -> A -> V(2, 0)
• V(2,1) -> B -> V(1, 1) -> A -> V(1,0)
• V(2,1) -> B -> V(1, 1) -> B -> V(0,1)
• V(2,1) -> B -> V(1, 1) -> C -> V(0,0)
• V(2,1) -> C -> V(1, 0)

Ya sólo queda calcular las probabilidades de cada evento de los 3 caminos que conducen a la victoria de E1. ¿Y de dónde las sacamos? Pues de las matrices que pusimos al principio, es justo por donde empezamos:

• V(2,1) -> A -> V(2, 0). P(A; 2,1) = 0.638889
• V(2,1) -> B -> V(1, 1) -> A -> V(1,0). P(B; 2,1)*P(A; 1,1) = 0.138889*0.361111 = 0.050154
• V(2,1) -> C -> V(1, 0). P(C; 2,1) = 0.222222

Por tanto, la probabilidad de que E1 gane la batalla que comenzó con 2 de sus tropas y una del rival es de 0.638889 + 0.050154 + 0.222222 = 0.911265.

La parte buena es que no ha sido tan difícil. La mala es que, a medida que crecen los ejércitos, el número de caminos posibles aumenta exponencialmente. Como tampoco estamos como para echar la tarde con esto, le pedimos a un ordenador que lo haga. El resultado que devuelve es la tabla siguiente, que representa tus probabilidades de victoria en una batalla completa en función de las tropas de las que dispones al comienzo (filas) y de las que dispone tu rival (columnas):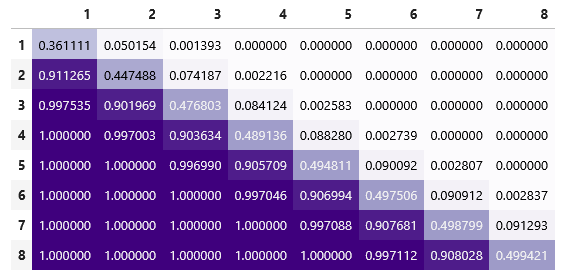



Bueno, y este es el resultado que quería comentar. En este juego ir con una tropa de ventaja proporciona en cualquier escenario aproximadamente un 90% de probabilidades de victoria. Si vamos con dos de ventaja ya nos ponemos en el 99%, es decir, victoria casi asegurada (aunque podamos perder alguna tropa por el camino). Es, por tanto, un sistema casi determinista en el que las batallas se ganan más por medio de las pujas de las subastas que con las espadas y las lanzas. Bruno Cathala y compañía no pretenden que doblegues a tus rivales a golpe de dado, sino que los ahogues gestionando tus ingresos y forzando las pujas para que cada mísera nueva tropa que recluten la hayan pagado al precio que merece vencer una batalla. Y ya puestos, ¿para qué están entonces los dados? Pues porque en este juego, a diferencia de en los mitos griegos, a veces se puede escapar del destino, y eso siempre es divertido.

A mi es un juego que me encanta. Sí que es verdad que es laaargo y no sale mucho a mesa por ese motivo, pero lo encuentro muy tenso y temático.
En alguna ocasión, un Drácula especialmente sibilino puede llegar a resultar frustrante para los cazadores si se pasan unos turnos sin pillarle el rastro, pero ¡qué narices! esa sensación es parte del viaje. Yo recuerdo todas mis partidas súper satisfactorias para los dos bandos.

No obstante, le echaré un ojo a los cambios propuestos, a ver por dónde van.
Muchas gracias

He recibido un enlace a un Kickstarter de un juego que por algún motivo ha despertado mi curiosidad. Se llama Aural Battle y trata de simular el típico combate entre entrenadores de Pokémons, pero sin pagar a Nintendo. Me ha llamado la atención que es un juego cerrado (nada de cartas coleccionables o cosas por el estilo), pequeño, que parece que simula bien lo que viene siendo una batalla pokemon y que parece bastante estratégico.



No tengo experiencia en este tipo de juegos y me surge la duda de si toda la información disponible (tipos de los bichos, vida, velocidad, objetivos, ataques...) no generarán demasiado AP y harán los turnos insufriblemente lentos. Lo mismo pero al revés: ¿serán evidentes las acciones a tomar (p.ej. atacar siempre a la criatura que presenta debilidad frente a tu ataque y cosas así)? Tampoco sé si es un planteamiento novedoso o si estas mecánicas ya están requetecubiertas por otros juegos del mismo estilo.

Sin más, abro el tema por si alguien quiere dar su opinión. Las reglas están disponibles en la página del KS y se puede imprimir una demo o jugarlo en Tabletop Simulator.

Enlace al KS:
https://www.kickstarter.com/projects/dayoscript/aural-battle/description
Print&Play y reglamento:
https://mega.nz/file/eFAXRKRA#_fIOQ_HLXOvPERY3eMj4SOYT9TqvUY4p6jgVng8qjyY

¿No hay limite de sacerdotisas que un jugador puede tener? Porque en el primer turno un jugador ya tiene 4 sacerdotisas y ya es imposible luchar contra eso...

Por lo que dices no fue tu caso, pero acumular sacerdotisas no tiene por qué ser necesariamente sinónimo de pasar el rodillo por el tablero. Por ejemplo, en nuestra última partida un jugador no tenía acceso a muchas cornucopias, así que se centró en una economía de sacerdotisas (llegó a acumular 7 u 8 ). Aunque era muy competente en las subastas, luego le faltaba cash para pagar movimientos o comprar tropas, así la partida se mantuvo ajustada hasta el final.

También ten en cuenta que las sacerdotisas del mapa sólo se consiguen la primera vez que tomas control de su área (no se cobran cada turno como las cornucopias).

Me descoloca un poco el arte de estos juegos.

En BGG hay doscientos millones de preguntas y aclaraciones de cómo funcionan muchas cosas. No sé si la gente es lerda o si realmente el juego deja muchas lagunas y libre interpretación.

Por ejemplo ¿se pueden mover tropas de una zona de una isla a otra zona de la MISMA isla, que no esté adyacente pero esté conectada vía barcos? Como las dos esquinas de un croissant pasando por una cadena de barcos en su playa/bahía, habiendo otra zona de tierra entre ambas esquinas, quedando sin adyacencia entre ellas, para imaginárnoslo. Hay quien interpreta las reglas diciendo que sí se puede, otros que no, que sólo se puede si das el salto a una segunda isla... Luego que si en el movimiento heróico es diferente, que si patatín que si patatán. Un follón. Y ya no hablemos de reglas específicas de cada monstruo o héroe.

En la bgg se han venido un poco arriba tratando de limar cualquier mínima duda, cruzando traducciones y aplicando la lógica aristotélica a cada frase del reglamento. Han elaborado unas FAQs no oficiales que más bien parecen las típicas guías de referencia de FFG. La mayoría son aclaraciones a situaciones muy atípicas o interacciones entre criaturas, héroes, etc cuya resolución se deduce del reglamento normal.

Sí que hay algunos puntos concretos que merecen aclaración. Parece que se los han pasado a Catala y se propone resolverlos. Por ejemplo, en el caso que comentas, ha dicho que se trata de una errata en el reglamento: Sí es posible moverse por barco entre áreas de una misma isla, que parece lo más consistente con las reglas de movimiento.

Una pena que la redacción del manual y la carta (al menos en español) sea tan ambigua. Cuando presentaron el poder de la Hidra durante la campaña (actualización #34), el texto que pusieron fue:

• During the Income Phase, multiply the income of the Zone occupied by the Hydra by 2.
• In Phase 4, after paying its maintenance cost, you can destroy a troop or fleet in its zone or one of its neighboring zones. If you do, add 1 Horn of Plenty to its zone.

Además, en los propios comentarios, los reponsables aclararon que "its zone" se refería a "the Hydra's zone".

Por tanto, las conclusiones serían:

• Que primero hay que pagar el coste de mantenimiento y, si se hace, se aplica el efecto
• Que la ficha de prosperidad se va a la casilla de la Hidra, lo que la hace muy poderosa ya que comba con su capacidad de duplicar ingresos

Realmente me parece un bicho muy interesante al que nunca dejaría escapar. Te viene tan bien que esté en una de tus zonas para cobrar sus jugosos ingresos que, si en un momento dado te quedas sin enemigos cerca, te puedes ver tentado a que se coma a tus propias tropas con tal de seguir cobrando. Otra opción es usarla para limpiar zonas vecinas antes de conquistarlas. Hagas lo que hagas, a pocos turnos que la puedas mantener en el tablero, creará una anomalía de cornucopias en el mapa que atraerá irremediablemente las codiciosas miradas de todos tus enemigos.

Hemos echado la primera partida a cuatro. Nadie en la mesa tenía experiencia con la versión anterior, pero ha sido fácil de explicar y no han surgido apenas dudas durante la partida. En total ha durado un poco menos de tres horas.

La verdad que la partida ha sido muy divertida y dinámica, con mucha interacción tanto en las pujas como en el campo de batalla. Ha habido distintas estrategias, unas más centradas en la economía, otras más expansivas... pero al final, el juego parece que predispone bastante al oportunismo y a la adaptación constante. Nos han parecido especialmente divertidos los efectos de las criaturas mitológicas, que irrumpían en el terreno desbaratando planes y obligando a repensar las estrategias. Por otro lado, a cuatro jugadores es casi imposible defender todos los frentes, lo que ayuda a mitigar un posible efecto bola de nieve mediante pequeñas alianzas puntuales que nunca fueron muy duraderas por los motivos comentados.



Las pujas tienen su intríngulis y todos nos hemos llevado sorpresas desagradables al perder al dios que más necesitábamos por no haber sabido leer bien las intenciones de los demás. Hay tantas posibilidades que es difícil saber lo que tiene en la mente cada jugador. Quizás creas que alguien no tiene interés en los poderes de un dios, pero resulta que puja a tope por él porque quiere ser el primero en comprar criaturas o porque le asusta que un rival pueda hacerse con su control.

Como ejemplo, en los compases finales de la partida apareció pegaso en la fila de criaturas. Pegaso te permite aerotransportar tropas de una casilla a otra sin necesidad de barcos ni dinero. La aparición de esta carta me inspiró tal amenaza que pujé todo lo que pude por el primer dios de la fila (Poseidón) para evitar que mi rival más directo pudiese comprar a pegaso en primer lugar y atacarme con él. La realidad, según me confesó posteriormente, es que su plan pasaba por hacerse con Poseidón para recuperar una isla que había perdido turnos atrás y que no tenía ningún interés en pegaso. Al haberle dejado sin Poseidón, pasó al plan B, acabó haciéndose con pegaso (yo me quedé sin dinero para comprarlo y no logré convencer a ningún otro jugador de que lo hiciera) y conquistó mi metrópolis. Como en las tragedias griegas, al intentar escapar de mi destino, terminé encontrándome con él.



Respecto a los dioses, al principio de la partida Hera es muy fuerte (todos los dioses dan la posibilidad de usar Héroes para desplazar tropas, pero Hera es la única que te permite reclutar uno), mientras que Atenea apenas te da posibilidades de desarrollarte económicamente. No obstante, aunque pueda parecer que algunos dioses son más poderosos que otros, la gracia del sistema de subastas es que ajusta, de forma muy orgánica, el coste de cada uno al valor que tienen en cada momento de la partida. Eso nos ha gustado como funciona. También nos ha dado la sensación de que Apolo no es el patito feo que aparenta y que más de una vez podría ser tu primera opción para ponerte fuerte antes de rondas clave. 

En resumen, todos lo hemos pasado muy bien. Tanto vencedores como vencidos hemos estado en la pugna y hemos disfrutado de algún turno de gloria, con lo que nos hemos ido para casa con muy buen sabor de boca. Ganas de repetir por parte de todos.